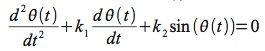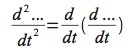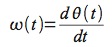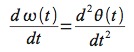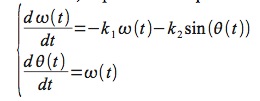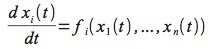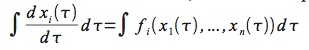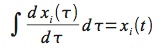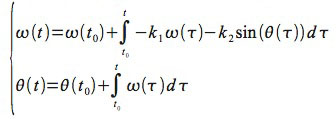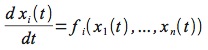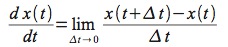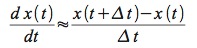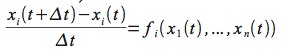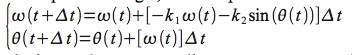Per informazioni, chiarimenti, consulenze:
Email: lmari_at_liuc.it
Telefono: 0331 572228
Se nel primo esempio siamo partiti da una soluzione a tempo discreto, dunque una soluzione α nello schema, nella descrizione della dinamica di sistemi fisici si assume tradizionalmente l’ipotesi di tempo continuo: la base per la ricerca di una soluzione a tempo globale, β o δ,è dunque in tal caso un’equazione differenziale, cioè una soluzione γ. Si spiega così l’importanza che le equazioni differenziali e i metodi per la loro soluzione hanno avuto nelle scienze fisiche da quando, a partire da Galileo e soprattutto Newton, si sono presi in esame problemi di dinamica dei sistemi, inizialmente in meccanica, poi termodinamica, elettromagnetismo, …
Per mostrare concretamente questo ruolo delle equazioni differenziali, introduciamo un esempio tratto dalla fisica elementare. Benché diverso per ambito disciplinare – meccanica invece di economia – e base di partenza – tempo continuo invece di tempo discreto –, vedremo le analogie tra questo esempio e il precedente: come fossero due facce di una stessa medaglia (un avvertimento: nelle righe che seguono c’è un po’ di matematica; la buona notizia per il lettore poco avvezzo a derivate e integrali è che la loro presenza è introdotta soprattutto per mostrare che le tecniche computazionali disponibili oggi consentono di non doversene occupare; vale quindi forse la pena di dar loro un’occhiata...).
Il secondo esempio
Consideriamo un pendolo, come quello schematizzato nella figura:
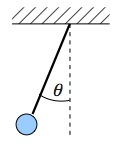
e supponiamo di essere interessati a descrivere la posizione angolare del pendolo stesso nel tempo, cioè l’andamento della variabile θ(t). Nei libri di fisica troviamo l’equazione appropriata:
una ODE del secondo ordine (cioè che contiene fino alla derivata seconda della funzione da integrare). Si tratta di un’entità non facilmente trattabile con tecniche analitiche (diciamo: le competenze che si acquisiscono nel corso di Analisi 1 nei corsi di laurea di fisica o matematica non sono sufficienti...), ma con pochi e semplici cambiamenti possiamo meglio metterne in evidenza le caratteristiche. L’unica nozione richiesta è la linearità della derivata, cioè il fatto che la derivata seconda è uguale alla derivata della derivata:
Se allora introduciamo una nuova variabile, definita come la derivata prima di θ(t):
si ha che:
In questo modo, la precedente equazione è trasformabile in un sistema di due ODE del primo ordine:
Quella che abbiamo appena applicato è una tecnica generale: attraverso l’introduzione di n-1 variabili intermedie, una ODE di ordine n può essere trasformata in un sistema di n ODE di ordine 1. Il risultato è dunque una soluzione γ, nella forma di un sistema di equazioni del tipo:
Tradizionalmente si affrontano problemi di questo genere cercando di ottenerne una soluzione δ, dunque in questo caso l’espressione analitica della funzione θ(t). La tecnica generale da impiegare è chiamata integrazione del sistema di ODE, dato che corrisponde a integrare entrambi i termini di ogni equazione:
e grazie al fatto che:
(cioè, in pratica, integrale e derivata sono operatori inversi) il nostro problema diventa:
A questo punto si comprende perché, come dichiarato sopra, una soluzione δ è non facilmente ottenibile: la prima delle due equazioni contiene il termine sin(θ(t)) e quindi è non lineare. Al proposito è interessante il seguente schema (tratto da un classico articolo di L. von Bertalanffy), in cui è evidenziato il caso corrispondente al nostro esempio (che il problema sia davvero “impossibile” o solo “molto difficile” cambia poco dal nostro punto di vista):

Si comprende dunque perché, allo scopo di cercare di ottenere comunque una soluzione δ, si possa scegliere di ridurre la complessità del problema linearizzandolo. Concretamente, si tratta di ammettere quella che in fisica si chiama approssimazione “per piccoli segnali”:
sin(θ(t)) ≈ θ(t)
(tecnicamente si tratta di sostituire la funzione sin(x) con il suo sviluppo in serie di Taylor arrestato al primo ordine, cioè approssimando in ogni punto una funzione con la retta tangente) e che, fino a che è accettabile (si confronti:
x= 0 sin(x) = 0 → uguali
x= 0,1 sin(x) = 0,0998... → uguali fino al terzo decimale
x= 0,2 sin(x) = 0,198... → uguali fino al secondo decimale
x= 0,3 sin(x) = 0,295... → uguali fino al secondo decimale
x= 0,4 sin(x) = 0,38 ... → uguali fino al primo decimale
e così via), rende il problema trattabile analiticamente.
Inquesta situazione si vede in azione il concetto, impiegato così frequentemente da essere divenuto una sorta di simbolo, di non-linearità come complessità, e quindi di linearizzazione come semplificazione.
Ma invece di cercare di ottenere la soluzione δ, è possibile seguire una strada diversa, percorrendo a ritroso la logica del primo esempio e ripartendo da un sistema di ODE del primo ordine, ognuna dunque della forma:
Invece di approssimare per linearizzazione, questa volta approssimiamo discretizzando il tempo, cioè trattando il differenziale dt come la differenza finita Δ t. In pratica, ricordando la definizione di derivata:
accettiamo che:
così che ogni ODE del primo ordine diventa (per semplicità dimentichiamo l’approssimazione e scriviamo “=” invece di “≈”):
A questo punto, è solo con un po’ di algebra elementare che si ottiene:
xi (t+∆ t) = xi (t ) + ƒi(xi (t), ... , xn (t))∆ t
che è la forma generica di una soluzione α.
In accordo a questa strategia, il nostro problema diventa perciò:
la cui soluzione può essere semplicemente trovata per via iterativa, a partire da valori dati per le condizioni iniziali θ(t0) e ω(t0), per esempio mediante un foglio di calcolo (si noti che in ogni passo del calcolo tutti i termini a destra del segno di uguale nelle due espressioni hanno valori noti, e quindi il calcolo stesso non presenta alcuna difficoltà). Ciò non conduce a un’espressione analitica per la funzione θ(t), e quindi a una soluzione β, ma solo alla successione di valori numerici θ(t0), θ(t0+Δt), θ(t0+2Δt), ..., ottenuta dunque per integrazione numerica.
Al di là del fatto estetico – è certamente più elegante una singola espressione analitica di una successione di valori numerici – la principale criticità di questo modo di procedere è dovuta alla necessità di calcolo replicato. In assenza di calcolatori programmabili ed efficienti, ciò rende questa strategia nei fatti impraticabile: si spiega così l’enfasi verso lo studio di metodi di integrazione analitica, che tuttora porta qualcuno a considerare l’analisi matematica, cioè appunto il calcolo differenziale e integrale affrontato per via analitica, quasi un sinonimo di matematica superiore. Ma nella situazione attuale, in cui la capacità di calcolo certo non manca, la via di trovare la soluzione di ODE mediante discretizzazione e integrazione numerica si propone come assai generale e flessibile, anche perché risulta applicabile a prescindere dalla linearità delle equazioni.
Se torniamo dunque al meta-problema con cui si era chiusa la prima parte – data una qualsiasi equazione a tempo locale, è sempre possibile trovare la sua corrispondente a tempo globale? – disponiamo ora di una risposta pragmatica: anche se la soluzione a tempo globale per via analitica non è nota (o non può essere trovata del tutto), se si accetta di operare a tempo discreto e per via numerica con pochi e semplici passaggi una ODE, lineare o meno, può diventare oggetto di calcolo previsivo e quindi di simulazione.
Rimane almeno un problema: a quali conseguenze conduce la trasformazione da tempo continuo a tempo discreto? Sotto quali condizioni la previsione rimane di qualità sufficiente? L’esplorazione di questo problema ci condurrà a scenari sorprendenti, finalmente davvero nel dominio della complessità.