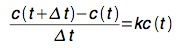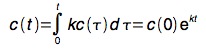Per informazioni, chiarimenti, consulenze:
Email: lmari_at_liuc.it
Telefono: 0331 572228
Premessa
L’analisi di (modelli di) sistemi dinamici, e quindi lo studio dell’andamento nel tempo di loro variabili è il contesto di base in cui si tratta di complessità anche in termini formali. Poiché almeno in certi casi la qualità e la quantità della matematica necessaria per seguire tale analisi (se non per svilupparla da sé) la rendono comprensibile anche senza competenze particolarmente sofisticate, può essere interessante dare un’occhiata a qualche esempio al proposito. Le nozioni acquisite e le considerazioni sviluppate saranno applicabili, almeno in linea di principio, anche a situazioni più complesse.
Tutto quello che occorre per cominciare il nostro percorso è una certa dimestichezza con le nozioni di variabile e funzione: assumiamo che lo stato di un sistema (un concetto che diamo qui per primitivo) sia caratterizzato in ogni istante dai valori di una o più variabili x1,..., xn che in generale variano nel tempo, e sono quindi considerabili funzioni del tempo, xi=xi(t). Si possono allora studiare problemi così strutturati:
- assumendo che siano conosciuti i valori xi(t0) delle variabili di stato in un certo “istante iniziale” t0,
- inferire i valori xi(t) in istanti t successivi a t0.
Se t0 è il presente, così che i valori xi(t0) potrebbero essere misurati sul sistema in esame, e quindi ogni t > xi(t0) è un istante futuro, il problema che stiamo ponendo è dunque di previsione. L’inferenza può essere compiuta leggendo l’oroscopo o simili (spesso addirittura prescindendo dalla conoscenza dello stato attuale del sistema: l’oroscopo è generalmente formulato nella forma: “sarai...”, e non: “se adesso sei..., allora sarai...”), oppure in accordo alla lezione che la fisica, da Galileo e Newton in poi, ci ha insegnato. E’ naturalmente in questa seconda direzione che seguiremo il nostro percorso, che comincia con un problema che forse è addirittura paradigma di semplicità, ma che ci fornirà alcune basi per le tappe successive.
Il primo esempio
Supponiamo che all’istante iniziale t0 sia stato depositato in banca un capitale c = c(t0) (non importa il riferimento di t0 al calendario, se ciò sia successo un anno fa o succederà fra un anno: si imposta così il problema come tempo-stazionario e in conseguenza possiamo porre per semplicità t0 = 0), e che sia stato concordato che a ogni intervallo di tempo ∆t, per esempio ogni anno, la banca paghi gli interessi sul capitale a tasso costante k > 0, così che gli interessi pagati sul capitale c dopo un intervallo ∆ t saranno c∆ t).
Una nota: poiché siamo interessati qui alla struttura del problema e della sua soluzione, e non ai valori specifici che se ne potrebbero ottenere, per semplicità tralasceremo le unità di misura per le variabili in gioco.
Ipotizzando che gli interessi siano interamente reinvestiti nel conto e che il conto non sia oggetto di versamenti né di prelievi, la dinamica del sistema risulta indipendente da elementi esterni al sistema stesso: il capitale evolve in modo autonomo, cioè senza essere influenzato dall’ambiente esterno, cosa che ne rende la previsione particolarmente semplice (senza questa ipotesi, e dunque descrivendo il sistema come aperto, si danno due opzioni, in base al fatto di assumere nota la successione dei versamenti e dei prelievi o meno: accenneremo nel seguito alla possibile strategia di soluzione da seguire in questi casi).
Si pone allora il problema di previsione del capitale c(m∆t) sul conto all’istante m∆ t, per m³1, dunque per esempio dopo m anni (il problema generale richiederebbe di prevedere c(t0+m∆ t), ma ricordiamo che abbiamo assunto t0 = 0).
La dinamica di questo sistema è descritta da:
nuovo capitale = capitale attuale + interessi = capitale attuale + tasso di interesse ´ capitale attuale
cioè:
c(t+∆ t) = c(t)+kc(t)
Prima di proseguire, consideriamo la struttura di questa equazione. Pur nella sua evidente semplicità, essa differisce dalle usuali equazioni algebriche per due motivi:
- la sua soluzione è costituita non da un numero, ma da una funzione, c(t);
- tale funzione compare più volte nell’equazione, in riferimento a valori diversi della sua variabile indipendente, il tempo t.
Per queste ragioni, possiamo chiamare “diacronica” (cioè “a tempo che passa”, in contrapposizione a “sincronica”, cioè “a tempo congelato”) questa equazione. Le equazioni diacroniche sono lo strumento di base per calcolare previsioni.
E’ opportuno generalizzare da subito l’equazione che abbiamo appena scritto, nell’ipotesi che gli interessi possano essere pagati, e quindi depositati sul conto, anche con una frequenza diversa da quella usata per stabilire il tasso di interesse. Per esempio k potrebbe essere calcolato su base annuale, e gli interessi pagati ogni sei mesi. Il modo più semplice per descrivere questa situazione è di adottare implicitamente il periodo in riferimento a cui è stabilito k come unità di misura del tempo, così che, per esempio, sei mesi corrisponde a ∆t = 0,5. Gli interessi pagati ogni ∆ t non sono perciò kc(t), ma la frazione di essi (supponendo ∆ t<1) maturata, cioè kc(t)∆ t.
Questo problema è dunque caratterizzato da:
capitale iniziale: c(0)
tasso di interesse nell’unità di tempo: k
periodo di pagamento degli interessi: ∆ t
capitale al periodo t+∆t: c(t+∆t) = c(t)+kc(t)∆ t = (1+k∆ t)c(t)
cioè:
c(t+∆t) = kc(t)
avendo definito:
k := 1+k∆ t
Per trovare la soluzione c(m∆ t) al variare di m≥1, si può operare per iterazione:
t0 = 0 → c(0)
t1 = ∆t → c(t1) = kc(0)
t2 = t1+∆ t = 2∆ t → c(t2) = kc(t1) = k2c(0)
...
tm = tm-1+∆t = m∆ t → c(m∆t) = kmc(0)
Per ragioni che saranno chiare poco più avanti, chiamiamo:
c(t+∆t) = c(t)+kc(t)∆t soluzione α
c(m∆t) = (1+k∆t)mc(0) soluzione β
Ripartendo dalla soluzione å, con un minimo di algebra si ottiene:
Il termine a sinistra è il rapporto incrementale della funzione c(t) (in pratica, come varia la funzione al variare della sua variabile indipendente) e per valori di ∆t decrescenti approssima sempre meglio la derivata di c(t). Al limite, per ∆t→0, e dunque ipotizzando che gli interessi siano pagati istantaneamente, non appena sono maturati, si ottiene:
cioè un’equazione differenziale ordinaria (ODE, ordinary differential equation) del primo ordine (contiene solo una derivata prima), la cui soluzione, facilmente ottenibile per integrazione analitica, è:
- Chiamiamo:
soluzione γ
soluzione δ
Abbiamo dunque ottenuto quattro soluzioni strutturalmente distinte per lo stesso problema, caratterizzate per l’ipotesi che il tempo vari in modo discreto (soluzioni α e β) o continuo (soluzioni γ e δ), e per la scelta di consentire una previsione a tempo locale (cioè “solo un istante in avanti”: soluzioni α e γ) o globale (cioè in qualsiasi istante successivo a quello iniziale: soluzioni β e δ). In sintesi:
|
|
Tempo discreto |
Tempo continuo |
|
Tempo locale |
α: c(t+∆t) = c(t)+kc(t)∆ t |
γ: |
|
Tempo globale |
β: c(m∆t) = (1+k∆t)mc(0) |
δ: c(t) = c(0)ekt |
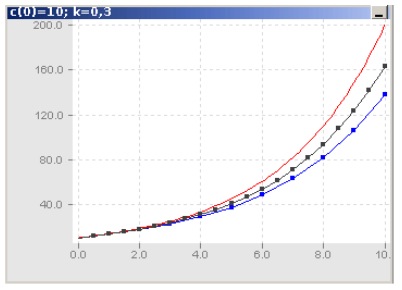
Come ci si può aspettare e come mostra il grafico che segue, la soluzione β si avvicina sempre più alla soluzione δ mano a mano che ∆t si avvicina a zero.
Le relazioni operative tra queste soluzioni sono:
|
|
Tempo discreto |
Tempo continuo |
||
|
Tempo locale |
α |
– passaggio al limite → ← discretizzazione – |
β |
|
|
|
| iterazione ↓ |
|
| integrazione ↓ |
|
|
Tempo globale |
β |
|
δ |
|
Le soluzioni d sono paradigmatiche dello stile di previsione derivato dalla meccanica classica: a tempo continuo – da Newton e Leibniz in poi – e globale – grazie al lavoro dei matematici che hanno fornito soluzioni al problema dell’integrazione analitica di equazioni differenziali.
E’ evidente la maggiore generalità delle soluzioni a tempo globale rispetto a quelle a tempo locale: le prime consentono infatti, con un unico calcolo, di prevedere il valore delle variabili di stato in un arbitrario istante di tempo e non solo “nell’istante successivo”. D’altra parte, nell’impostare un problema si parte generalmente da equazioni a tempo locale, che devono essere trasformate in equazioni a tempo globale attraverso un’operazione analitica di iterazione (se a tempo discreto) o di integrazione (se a tempo continuo).
Si pone perciò il meta-problema: data una qualsiasi equazione a tempo locale, è sempre possibile trovare la sua corrispondente a tempo globale?